ما بين الرياضيات واللغة

من واجبي أن أتحدث عن نعمة من نعم الله السابغة عليّ، ذلك أن من الإفادات التي استفذتها من دراسة الرياضيات والتعمق فيها والعودة إليها من آن لآخر أنني أصبحت قادراً على فحص صدقية النصوص بأسهل ما يمكن، ذلك أنني لا أشغل نفسي بتشخيص المقدمات والنتائج على النحو الذي يمارس به المناطقة هذه المهمة، ولكنني بالتدريب العقلي المستمر في صباي أصبحت أحول كل قضية أمامي إلى رموز رياضية من قبيل س وص وع وعمليات حسابية أو جبرية من قبيل الجمع والطرح والضرب والقسمة والتعويض والنقل والتعبير عن الشيء الواحد بأكثر من رمز، وباختصار شديد يقرب مثل هذا المعنى للقارئ بسرعة فإنني أعترف بأن بسطاء الريف يستطيعون بسليقتهم أن يمارسوا صورة مبسطة من هذا حين يعتبرون تقسيم التركة بين أربعة أبناء وأربع بنات بمثابة قسمة على ستة وذلك باعتبار أن س =2 ص، ومن ثم فإن 4س + 4 ص = 6 س أو يساوي 12 ص وهكذا.

 

طبعا فإن الحديث بمثل هذا المثل المتكرر يعتبر اختزالا كبيرا للمعنى الذي أقصد الحديث عنه، وهو ما يجعل بعض المستمعين إليّ يقولون: لا تخدعنا يا دكتور، لكني أحب أن أعترف أن الأمور الرياضية في جوهرها لا تتعدى هذا المثل بأي حال من الأحوال مهما كان تعقيد وتركيب وتركم المعادلات الخاصة بالتفاضل والتكامل والاحتمالات وحساب المثلثات والهندسة الفراغية و.. الخ. ومن الطريف أن معايشة الحسابات الجبرية والهندسية تجعل الانسان ذا القدرات العقلية المعقولة (لا الفارقة) يكتشف كثيراً من القواعد الرياضية بسهولة وذلك على نحو ما اكتشف فيثاغورث نظريته، وعلى نحو ما اكتشف المعاصرون له من الرواد نظرياتهم الكثيرة وهي نظريات عبقرية رغم بساطتها وبسيطة رغم عبقريتها.

 

ومن هذه الحقائق التي أعجب بها بعض أساتذتنا وأنا اذكرها بتلقائية ذات مرة أنك إذا كنت تملك على سبيل المثال حبلا طويلا وأردت أن تجعله محيطا لشكل رباعي منتظم بحيث يعطيك أفضل مساحة فإن أفضل الخيارات لك هو أن تختار شكل المربع وليس شكل المستطيل، وعلى سبيل المثال إذا كان هذا الحبل 20 مترا فإنك إذا صنعت به إطار مربع فإنك تحصل على مساحة 25 مترا مربعا وهي المساحة التي لا يمكن لك أن تحصل عليها من أي مستطيل تصنعه بهذا الحبل ذلك أنك لو جعلت طول المستطيل 6 وعرضه أربعة أمتار فإنك تحصل على مساحة 24 مترا فقط وإذا جعلت طوله سبعة أمتار وعرضه ثلاثة أمتار فإنك تحصل على مساحة 21 متراً فقط، وإذا جعلت طوله ثمانية أمتار وعرضه مترين فإنك ستحصل على مساحة 16 مترا مربعا فقط وإذا جعلت طوله تسعة أمتار وعرضه متراً واحداً فإنك ستحصل على مساحة 9 متراً مربعا فقط بل إنك إذا جعلت عرضه نصف متر وطوله تسعة أمتار ونصف فلن تحصل إلا على مساحة أربعة أمتر ونصف مربع وهكذا وبهذه الطريقة فإن المساحة التي تحصل عليها من نفس المحيط تتفاوت ولا تصل إلى قمتها أو أقصاها إلا في حالة المربع.

ما بين أقصى مساحة وأدنى مساحة

وبالطبع فإنك لست على الدوام راغبا في أن تحصل على أقصى مساحة، فهناك في بعض الأحوال ما يستدعي الحصول على أقل مساحة وهكذا. ولمثل هذه القاعدة تطبيقات مهمة في بناء المساكن في التجمعات الجديدة حيث يكون المالك الجديد ملزما بمساحة محددة لا يتعداها من المساحة الكلية التي اشتراها، ومن ثم فإن الحاجة إلى استغلال الواجهة تجعله يلجأ بذكاء إلى تطويل ضلع المستطيل المقابل للواجهة المتميزة، والعكس صحيح، وكما تنطبق هذه القاعدة على المربع والمستطيلات فإنها تنطبق على الدائرة والأشكال البيضاوية التي هي من الدائرة بمثابة المستطيل من المربع.

أتقدم خطوة للأمام لأذكر قصة شجعني عليها والدي رحمه الله بما لا يمكن تقديره من التشجيع الصادق المحب الذي كان رحمه الله يفيض عليّ منه بما لا يتصوره العقل البشري وبما لم أجده من إنسان آخر لأي ابن له ولا لأي معجب ولا على سبيل النفاق لصاحب السلطة، فقد كنا نمر في طريقنا على أحد معامل تصنيع الصفائح المخصصة للمواد الغذائية وبصفة خاصة الجبن والزبد والطحينة وزيت السمسم الذي كان أحد المصانع الصغيرة يُنتجه في مدينتنا استمراراً لقدرتنا التصنيعية (التي تضاءلت بعد ثورة 1952 وما فرضته من تأميم لا مبرر له لكثير من الصناعات الصغيرة)، ووجدني والدي عليه رحمة الله أقول للصانع هل لي أن أدلك على طريقة تجعل لوح الصفيح الخام يعطيك سعة أكبر من هذه الصفيحة التي تصنعها الآن؟ كان الرجل رحمه الله يحبني، فقال لي ببساطة شديدة: تفضل فرسمت له أبعاد العلبة التي اقترحها، ولم تكن التكنولوجيا ساعتها تسمح بتطويع الصفيح إلا بالضغط عبر “أداة تكسير يدوية مجهدة” لكن الرجل بأريحية كريمة لم يجد مانعا من أن يضيع ساعة من وقته في إعادة ضبط الماكينة البسيطة التي لا يملك غيرها وفي احتمال التضحية بلوح كامل من الصاح كامل لينفذ هذه التجربة، وكان هذا الرجل من الذكاء الفطري بحيث إنه لم يكتف بما نجربه من حسابات التكعيب بضرب الطول في العرض في الارتفاع ولكنه صمم على أن يملأ الصفيحة بالماء ليرى الحقيقة، وإذا به يجد أن ما كان يملأ صفيحة من المقاس الذي تعود إنجازه قد تم استيعابه فيما يقرب 80% فقط من الصفيحة الجديدة التي تم تشكيلها بالمقاسات التي ذكرتها له. وكان السر فيما ذكرت هو الفارق بين المكعب ومجموع متوازي المستطيلات.

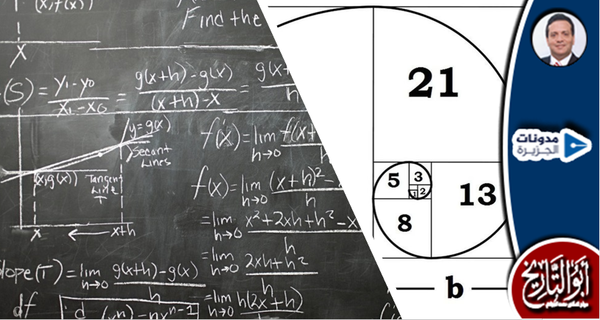
قصة النسبة الذهبية

مرت عقود على هذه الواقعة وأصبحت عضواً في مجمع اللغة العربية وورد مصطلح النسبة الذهبية ضمن المصطلحات فاعترض أكثر من أستاذ من أساتذتنا من الذين يمارسون النقد الأدبي ومن الذين يمارسون تعليم الفلسفة على ورود مثل هذا الوصف ضمن نص علمي في مصطلح يصف شيئاً آخر محددا، وكانت وجهة نظرهم المنطقية أن هذا النص الذي يعترضون عليه يتضمن ما يُسمى في العلم بالحكم القيّمي، وهو أمر لا يجوز في مصطلح علمي أو نص معجمي، وإذا بالأعضاء يفاجئون بي مندفعا لأدافع عن النسبة الذهبية، وأصفها بأنها علم وإن كانت في الوقت ذاته بمثابة حكم قيمي بالفعل، وقيمي بالرقم، من ناحية القيمة العددية، ومن ناحية القيمة العملية وهي قيمة فنية وفلسفية أيضا !

 

وبالطبع فإن أساتذتنا فوجئوا بهذا التدخل الصارخ في المناقشة فطلبوا من لجنة الرياضيات أن تتولى اللجنة الرد، فما كان من أستاذ أساتذة الرياضيات عليه رحمة الله (رغم ما كان يبدو من جفاف علاقتنا) إلا أن نظر إليّ بعطف قائلاً: فوضناك. فلما انتهيت من شرح قصة النسبة المذهبية بالطريقة الجوادية التي تخلط الواقع بالعلم دعا لي أساتذة الفلسفة بأن يزيدني الله علما بالرياضة التي أخذت من اللغة العربية ما تريد من دون استئذان ولا مقابل. أظن أن من حق القارئ أن اذكر له أن النسبة الذهبية إذا ما حسبت طبقا للنظام البشري ستكون مقربة حسب ما يسمح به السياق فلو اننا نقتصر على كسر من المائة فقط فإنها 1.61 ولو أننا نقتصر على كسر من الألف فهي 1.618 وهكذا قبل أن أذكر تعريفها الرياضي أشير إلى أنها مستعملة في هرم خوفو كما أنها مستخدمة في البنتاجون الذي أقيم على شكل خماسي نسبة طول الوتر فيه إلى طول الضلع هي النسبة الذهبية، بل إن ليوناردو دافنشي نفسه (1452-1519) أشار إلى كتاب لأحد الرهبان بعنوان “التناسب الإلهي” تحدث عن الخصائص العجيبة رياضيا وجماليا لهذه النسبة، وفيما يخص المسلمين فإنهم في كثير من زخارفهم عرفوا هذه النسبة بل إن هناك دراسات كثيرة متعلقة بالكعبة المشرفة والنسبة الذهبية، ومنها أن النسبة بين بعد الكعبة عن القطب الشمالي وبعدها عن القطب الجنوبي تساوي النسبة الذهبية بالضبط، ولا يمكن لمن بناها أن يعرف هذه النسبة إلا بإلهام الله سبحانه وتعالى.

التعريف الرياضي

ونأتي الآن إلى التعريف الرياضي للنسبة الذهبية، فهي تتحقق عندما يكون مجموع عددين مقسوم على أكبرهما يساوي خارج قسمة أكبر العددين على أصغرهما، فإذا أردنا تعبيراً لغويا يعبر عن هذا المعنى الرياضي بدقة من دون الإحالة على كلمة أكبرهما وأصغرهما ويساوي ومجموع ومقسوم فإننا نجد الصياغة اللغوية الجوادية التي قادتنا إلى هذا الاستطراد وهي أنها تلك النسبة بين عددين “تتساوى نسبة أكبرهما إلى أصغرهما مع نسبة مجموعها إلى أكبرهما” والمعنى من هذه الصياغة الجوادية واضح، أن النسبة لن تتحدد بنفسها وإنما تتحدد حينما يكون هناك عددان منسوبان إلى بعضهما وبالطبع فكل عددين يمكن نسبتهما إلى بعضهما فينتج نسبة وعلى سبيل المثال النسبة بين 3 و2 = 150% لكن النسبة بين مجموعهما إلى أكبرهما 166% وهكذا فالنسبة ليست ذهبية. والنسبة بين 4 و3 = 1.33 لكن النسبة بين مجموعهما وأكبرهما 1.75 وهكذا فإننا نبتعد كلما زادت الأرقام عن النسبة الذهبية. وكذلك عندما تنقص الأرقام فالنسبة بين 2 و1 هي 200% والنسبة مجموعهما وأكبرهما أي بين 3 و2 هي 150% أما في حالة النسبة الذهبية حيث الرقمان هما 1.62 و1 فإن النسبة بين أكبرهما إلى أصغرهما هي 162% وبين مجموعهما 262 وأكبرهما 162 هي 162%

 

تليين الصياغات

ومن هنا جاءت الصياغة الجوادية القائلة ما نصه: تتساوى نسبة أكبرهما إلى أصغرهما مع نسبة مجموعهما إلى أكبرهما” وبالطبع فإن الشياكة اللغوية تقتضي وضع حرف الواو بدلاً من مع ولكن بعد أن نكون فهمنا النص على نحو ما فهمه أساتذتي في المجمع دعوا لي ولا يزالون يدعون . هل أزيدكم من الشعر بيتا أو بيتين، ها أنتم ترون الآن أساتذتنا وقد أمسك أغلبهم بالقلم والورق وكتب ما يريد أن يفهمه ويستوعبه من قصة هذه النسبة ثم استقر ذوقهم على قبول صياغتي اللغوية الدقيقة لهذا المعنى الرياضي وأصبحوا سعداء بقدرة اللغة على التعبير الدقيق وبقبول علماء الرياضيات للصياغة التي قدمتها وأقروها هم، باعتبارهم علماء اللغة.. قلت لأساتذتنا هل أستأذنكم بعد أن دعوتم لي أن تنسوا الرياضة الآن وتنظروا إلى الجملة العربية التي أمامنا لنتأمل كيف يمكن لنا أن نعيد صياغتها صياغات عربية أكثر رشاقة.. واستأذنت الرئيس أن نبقى مع النص في صمت مدة دقيقتين، ثم بدأت في طرح صياغات جديدة لكي يرى أساتذتنا صوابها من عدمه، وكان من هذه الصياغات على سبيل المثال:

– النسبة بين عددين، مجموعهما إلى أكبرهما كأكبرهما إلى أصغرهما

– النسبة بين عددين أكبرهما إلى أصغرهما كمجموعهما إلى أكبرهما.

وهكذا.. وكلما ذكرت نصاً من هذه النصوص وافق عليه الأعضاء مباشرة أو بعد سؤال يسير.

 

 

 

🔊 استمع إلى المقال

تم النشر نقلا عن موقع مدونات الجزيرة

لقراءة المقال من مدونات الجزيرة إضغط هنا

للعودة إلى بداية المقال إضغط هنا